字符串搜索算法

KMP 算法

KMP 算法是一种用于在一个主文本字符串 $S$ 中查找一个模式字符串 $P$ 的子串的算法.
KMP 算法的时间复杂度是 $O(\textrm{len}(S)+\textrm{len}(P))$.
KMP 算法的核心是构建一个部分匹配表, 用于在匹配失败时, 快速移动模式字符串.
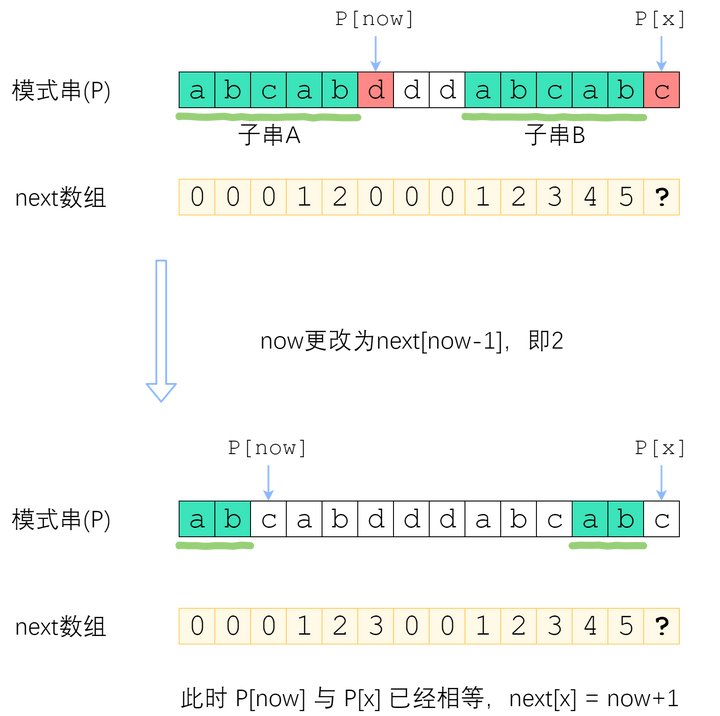
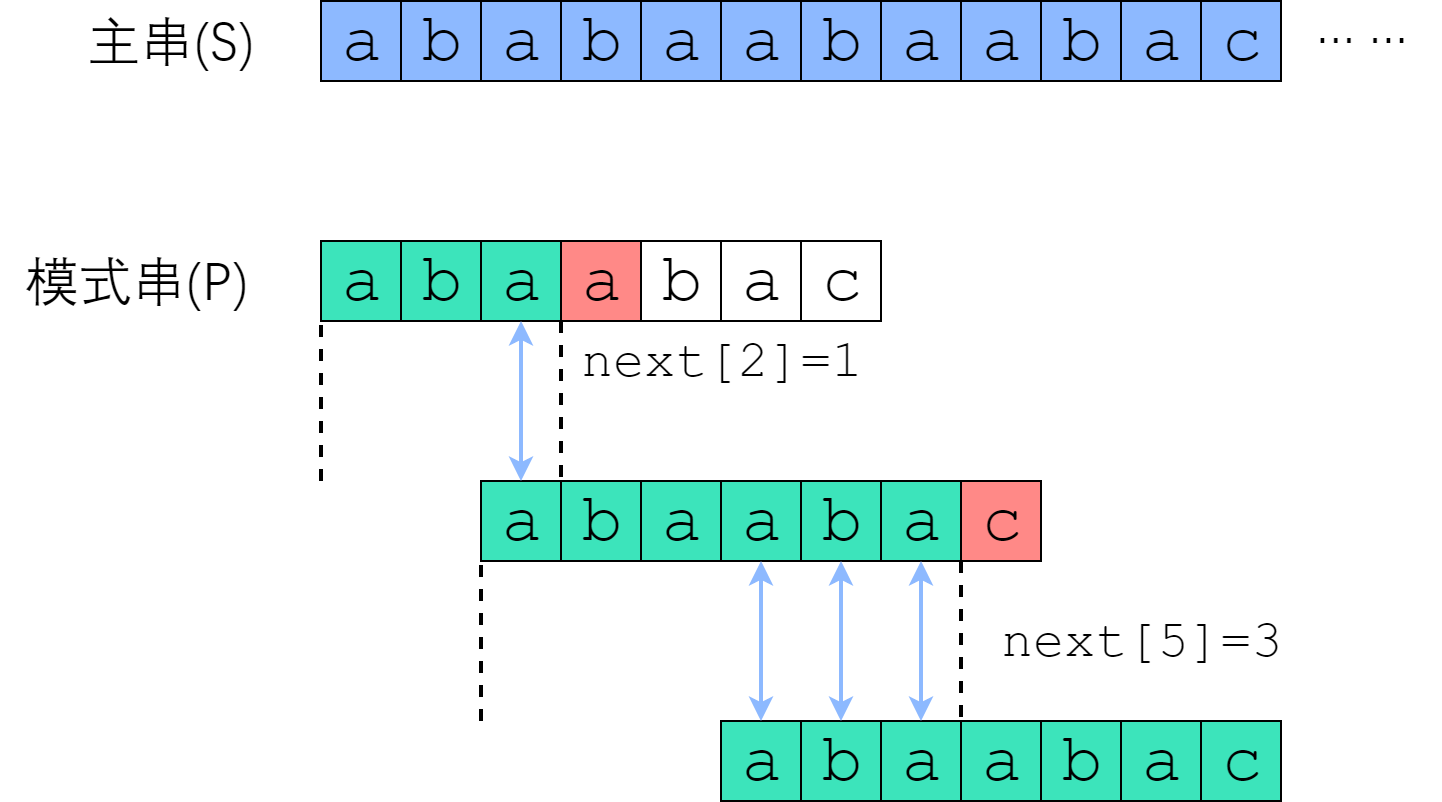
KMP 算法的部分匹配表(kmp_table)是一个数组, 数组的第 $i$ 个元素表示 P[:i] 的前缀和后缀的最长公共元素的长度.例如 P=abcabd, 那么 kmp_table(P)=[0,0,0,1,2,0]. 因此匹配到 P[5] 时, 如果不匹配, 那么直接从 P[table[4]]→P[2] 的位置开始匹配, 因为 P[3:5] 和 P[0:2] 是相同的字符串.

参考

1. 为模式字符串 $P$ 生成部分匹配表
   1. 初始化 table 为长度为 $P$ 的长度的数组, 初始值为 0. 初始化 $i$ 和 $j$ 为 1 和 0. $i$ 表示当前位置, $j$ 表示前缀的末尾位置.
   2. 循环直到 $i$ 到达 $P$ 的长度
      1. 如果 P[i] 和 P[j] 相等, 则 $j$ 向后移动一位, 记录 table[i]=j, $i$ 向后移动一位
      2. 如果 P[i] 和 P[j] 不相等
         1. 如果 $j>0$, 则 $j$ 移动到 table[j-1] 的位置. 因为可以确定 P[j-table[j-1]:j] 和 P[:table[j-1]] 是相等的, 所以可以直接从 table[j-1] 的位置开始匹配.
            
         2. 如果 $j=0$, 则 $table[i]$ 的值为 0, $i$ 向后移动一位
2. 在主文本字符串 $S$ 中查找模式字符串 $P$. $P$ 和 $S$ 的指针设为 0 位置.
   1. 如果当前字符匹配, 则 $P$ 和 $S$ 的指针各向后移动一位
   2. 如果当前字符不匹配
      1. 如果 $P$ 的指针在 0 位置, 则主文本字符串的指针向后移动一位
      2. 如果 $P$ 的指针 $j$ 不在 0 位置, 则 $P$ 的指针向后移动到 table[j-1] 的位置, 因为可以确定 P[j-table[j-1]:j] 和 P[:table[j-1]] 是相等的, 所以可以直接从 table[j-1] 的位置开始匹配.
         
   3. 循环直到 $P$ 的指针到达 $P$ 的末尾, 或者主文本字符串的指针到达主文本字符串的末尾.

def kmp_table(pattern):
    table = [0] * len(pattern)
    i, j = 1, 0
    while i < len(pattern):
        if pattern[i] == pattern[j]:
            j += 1
            table[i] = j
            i += 1
        else:
            if j > 0:
                j = table[j - 1]
            else:
                table[i] = 0
                i += 1
    return table

def kmp_search(text, pattern):
    table = kmp_table(pattern)
    i, j = 0, 0  # S匹配的位置, P匹配的位置
    while i < len(text):
        if text[i] == pattern[j]:
            i += 1
            j += 1
            if j == len(pattern):
                return i - j
        else:
            if j > 0:
                j = table[j - 1]
            else:
                i += 1
    return -1