概率统计问题
球盒问题
$n$ 个球放到 $m$ 个盒子中, 允许空盒子, 有几种放法?
解答 相当于 $n+m$ 个球放到 $m$ 个盒子中, 不允许空盒子
使用隔板法, 就是 $\operatorname{C}_{n+m-1}^{m-1}$
连续抛硬币
抛硬币, 出现正面的概率为 $p$, 抛到连续出现 $k$ 次正面为止, 抛的次数的期望是多少?
解答
简化问题
直到连续出现两次正面为止,平均要抛多少次才能结束游戏?
假设期望为 $\operatorname{E}(2)$. 递归. 首先先抛一枚硬币,如果是背面,那么需要重头开始;如果是正面,那么再抛一枚硬币,新抛的这枚如果也是正面,则游戏结束,如果是背面,那么又需要重头开始。
\[\operatorname{E}(2) = 1 + (1-p)\operatorname{E}(2)+p[1+p\times 0+(1-p)\operatorname{E}(2)] = \frac{1+p}{p^2}\]原问题
先抛掷 $\operatorname{E}(k-1)$ 次,得到连续的 $k-1$ 个正面,然后再抛一次,若是正面,则游戏结束;否则需要重头开始,也就是说又需要 $\operatorname{E}(k)$ 次。
\[\operatorname{E}(k) = \operatorname{E}(k-1) + 1 + p\times 0+(1-p)\operatorname{E}(k)= \frac{1+E}{p}=\frac{1}{1-p}\left(\frac{1}{p^n}-1\right)\]概率生成函数
定义 一个离散随机变量的概率母函数(probability generating function)是指该随机变量的概率质量函数的幂级数表达式。
\[G(z)=\operatorname{E}(z^{X})=\sum _{x=0}^{\infty }p(x)z^{x}\]- 概率 ${\displaystyle p(k)=\operatorname {Pr} (X=k)=\frac {G^{(k)}(0)}{k!}}$
- 期望 $\displaystyle \operatorname {E} [X]=G^\prime(1^{-})$
- 方差 $\operatorname {Var} (X)=G^{\prime\prime}(1^{-})+G^\prime(1^{-})-\left[G^\prime(1^{-})\right]^{2}$
- $k$-阶矩 kth raw moment ${\displaystyle \operatorname {E} [X^{k}]=\left(z{\frac {\partial }{\partial z}}\right)^{k}G(z){\Big |}_{z=1^{-}}}$
- 矩生成函数 Moment-generating function $M_{X}(t)=\displaystyle G_{X}(e^{t})$
原问题的概率生成函数
参考
记恰好 $n$ 次投掷硬币获得 $k$ 次连续正面的概率为 $P_{n,k}$ . 有 $P_{n,n}=p^n$, $P_{k,n}=0(k<n)$.
根据第一次投掷出翻面的次数 $i$ 分类讨论, 有
利用随机变量生成函数 $G_k(z) = \sum_{n=0}^\infty P_{n,k}z^{n}$. 有
\[G_n(z)[1-(1-p)z-\cdots-p^{n-1}(1-p)z^n]=P_{n,n}z^n=p^nz^n\] \[\begin{equation} \begin{split} G_n(z)=\sum_{n=0}^\infty P_{n,k}z^n & =P_{k,k}z^k+\sum_{n=k+1}^\infty P_{n,k}z^n=P_{k,k}z^k+\sum_{n=k+1}^\infty \sum_{i=1}^k p^{i-1}(1-p)P_{n-i,k}z^n \\ & = P_{k,k}z^k+\sum_{i=1}^k p^{i-1}(1-p)z^i\sum_{n=k+i}^\infty P_{n-i,k}z^{n-i} \\ & = P_{k,k}z^k+G_k(z)\sum_{i=1}^k p^{i-1}(1-p)z^i \\ & = p^kz^k + \frac{(1-p)(p^kz^{k+1}-z)}{pz-1}G_k(z) \\ & = \frac{p^kz^k(1-pz)}{1+p^kz^{k+1}(1-p)-z} \end{split} \end{equation}\]期望
\[\operatorname{E}(k) = G_k'(1^{-}) =\frac{1}{1-p}\left(\frac{1}{p^k}-1\right)\]方差
\[\begin{equation} \begin{split} \operatorname{var}(k) &= G_k''(1^{-})+G_k'(1^{-})-\left[G_k'(1^{-})\right]^2 \\ &= -\frac{2k}{p^k(1-p)}+\frac{(1+p^{k+1})(1-p^k)}{p^{2k}(1-p)^2}\end{split} \end{equation}\]期望和方差可以利用SymPy计算直接得到结果
1
2
3
4
5
6
import sympy as sp
k = sp.Symbol('k', integer=True, positive=True)
z, p = sp.symbols('z p', real=True, positive=True)
G = p**k*z**k*(1-p*z)/(1+p**k*z**(k+1)*(1-p)-z)
E = sp.simplify(sp.diff(G, z).subs(z, 1))
V = sp.simplify(sp.diff(G, z, 2).subs(z, 1) + E - E**2)
蓄水池抽样
从包含 $n$ 个项目的集合 $S$ 中选取 $k$ 个样本,其中 $n$ 为未知量
解答
- 从 $S$ 中抽取首 $k$ 项放入「水塘」中
- 对于每一个 $S[j] (j\ge k)$ 项:
- 随机产生一个范围从 0 到 $j$ 的整数 $r$
- 若 $r<k$ 则把水塘中的 $r$ 项换成 $S[j]$ 项
根据骰子向前走
一个人扔六面的骰子,数值1到6,扔到几就向前走几格,可以无限扔,问他恰好走到第2023格的概率
解答
骰子等概率的从前面 6 个格子走到这个格子
\[P_{n}=(P_{n-6}+P_{n-5}+P_{n-4}+P_{n-3}+P_{n-2}+P_{n-1})/6\]假设起点概率是 1, 经过起点前的点概率不存在.
\[P_{0}=1,P_{-1}=P_{-2}=P_{-3}=P_{-4}=P_{-5}=0\]列出转移矩阵为:
\[M = \left[\begin{array}{ll} &1&&&&\\ &&1&&&\\ &&&1&&\\ &&&&1&\\ &&&&&1\\ \frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6}&\frac{1}{6} \end{array}\right]^n\cdot\left[\begin{array}{ll}0\\0\\0\\0\\0\\1\\\end{array}\right]\]每次左乘一个转移矩阵, 得到的概率从 $P(i)\sim P(i+5)$ 变成 $P(i)\sim P(i+6)$. 从状态 $i$ 到状态 $i$ 的概率一定为 1, 因为是已经确定的, 要计算的只有 $i+6$.
要估算的话令此时的特征多项式为
\[λ^6-\dfrac{1}{6}(1+λ^2+λ^3+λ^4+λ^5) = 0\]因式分解得:
\[(6 λ^5+5 λ^4+4 λ^3+3 λ^2+2 λ+1)(λ-1)=0\]解得:
\[\begin{aligned} λ_1&=1\\ λ_2&=+0.294195+0.668367 i\\ λ_3&=+0.294195-0.668367 i\\ λ_4&=-0.375695+0.570175 i\\ λ_5&=-0.375695-0.570175 i\\ λ_6&=-0.670332\\ \end{aligned}\]也就是说 $M≈\dfrac{1}{7} (1 + {λ_1}^n+ {λ_2}^n+ {λ_3}^n+ {λ_4}^n+ {λ_5}^n+ {λ_6}^n)$
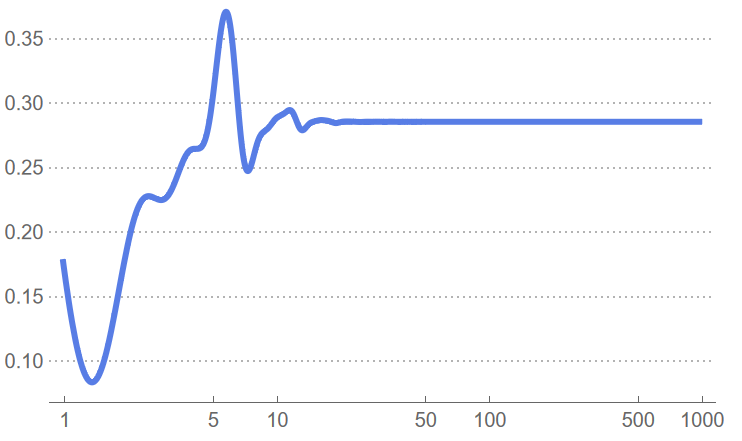
除了 $λ_1^n = 1$, 其他的模平方全部小于 1, 加上指数会全都变成 0, 显然就会收敛到 $\dfrac{2}{7}$
最终结果只和特征值有关, 和初值无关, 到达稳态之后是 100 还是 2023 还是 2024 都不怎么重要.
掷骰子的期望
一个公平的骰子, 平均掷多少次才能掷出连续的两个6?
解答
使用马尔科夫链, 设置3个状态:
- 状态0: 还没有掷出6
- 状态1: 刚掷出一个6
- 状态2: 刚掷出两个6
设从状态i到状态j的转移概率为 $P(i,j)$, 转移矩阵
\[M = \left[\begin{array}{ccc} \frac{5}{6} & \frac{1}{6} & 0 \\ \frac{5}{6} & 0 & \frac{1}{6} \\ 0 & 0 & 1 \\ \end{array}\right]\]设期望从状态i到达状态2的步数为 $E(i)$, 则有:
\[\begin{aligned} E(0) &= 1 + \frac{5}{6}E(0) + \frac{1}{6}E(1) \\ E(1) &= 1 + \frac{5}{6}E(0) + \frac{1}{6}E(2) \\ E(2) &= 0 \\ \end{aligned}\]第一行的意思是, 当我处于状态0时, 我需要掷一次骰子, 然后有 $\frac{5}{6}$ 的概率回到状态0, 有 $\frac{1}{6}$ 的概率转移到状态1.
联立方程组, 解得:
\[E(0) = 42, \quad E(1) = 7, \quad E(2) = 0\]因此, 平均掷42次才能掷出连续的两个6.
解法2. 参考吸收马尔科夫链的基本矩阵概念, 已知瞬态转移矩阵
\[\mathbf{Q}=\begin{bmatrix}\frac{5}{6} & \frac{1}{6} \\ \frac{5}{6} & 0\end{bmatrix}\]基本矩阵 $\mathbf{N}=(\mathbf{I}-\mathbf{Q})^{-1}$, 联立求解方程
\[\begin{bmatrix}a&b\\c&d\end{bmatrix}\begin{bmatrix}\frac{1}{6}&-\frac{1}{6}\\-\frac{5}{6}&1\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}\]得到
\[\mathbf{N}=\begin{bmatrix}36 & 6 \\ 30 & 6\end{bmatrix}\]从状态0开始, 到状态2结束, 中间状态0的期望步数为36, 状态1的期望步数为6, 那么一共42步. 注意这里的36, 包含了初始时刻的那一步.