谱聚类
来源: 刘建平Pinard
谱聚类(spectral clustering)是广泛使用的聚类算法,比起传统的K-Means算法,谱聚类对数据分布的适应性更强,聚类效果也很优秀,同时聚类的计算量也小很多,更加难能可贵的是实现起来也不复杂。在处理实际的聚类问题时,个人认为谱聚类是应该首先考虑的几种算法之一。下面我们就对谱聚类的算法原理做一个总结。
1. 谱聚类概述
谱聚类是从图论中演化出来的算法,后来在聚类中得到了广泛的应用。它的主要思想是把所有的数据看做空间中的点,这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高,通过对所有数据点组成的图进行切图,让切图后不同的子图间边权重和尽可能的低,而子图内的边权重和尽可能的高,从而达到聚类的目的。
乍一看,这个算法原理的确简单,但是要完全理解这个算法的话,需要对图论中的无向图,线性代数和矩阵分析都有一定的了解。下面我们就从这些需要的基础知识开始,一步步学习谱聚类。
2. 谱聚类基础之一:无向权重图
由于谱聚类是基于图论的,因此我们首先温习下图的概念。对于一个图 $G$,我们一般用点的集合$V$和边的集合$E$来描述。即为 $G(V,E)$。其中 $V$ 即为我们数据集里面所有的点 $(v_1, v_2,…v_n)$。对于 $V$ 中的任意两个点,可以有边连接,也可以没有边连接。我们定义权重 $w_{ij}$ 为点 $v_i$ 和点 $v_j$ 之间的权重。由于我们是无向图,所以 $w_{ij} = w_{ji}$。
对于有边连接的两个点 $v_i$ 和 $v_j$,$w_{ij} > 0$,对于没有边连接的两个点 $v_i$ 和 $v_j$,$w_{ij}= 0$。对于图中的任意一个点 $v_i$,它的度 $d_i$ 定义为和它相连的所有边的权重之和,即
\[d_i = \sum\limits_{j=1}^{n}w_{ij}\]利用每个点度的定义,我们可以得到一个 $n\times n$ 的度矩阵 $D$,它是一个对角矩阵,只有主对角线有值,对应第 $i$ 行的第 $i$ 个点的度数,定义如下:
\[\mathbf{D} = \begin{bmatrix} d_1& \ldots & \ldots \\ \ldots&d_2 & \ldots \\ \vdots & \vdots & \ddots \\ \ldots & \ldots & d_n \end{bmatrix}\]利用所有点之间的权重值,我们可以得到图的邻接矩阵 $W$,它也是一个 $n\times n$ 的矩阵,第 $i$ 行的第 $j$ 个值对应我们的权重 $w_{ij}$ 。
除此之外,对于点集 $V$ 的的一个子集 $A \subset V$,我们定义:
\[|A|: = \text{子集}A\text{中点的个数}\] \[vol(A): = \sum\limits_{i \in A}d_i\]3. 谱聚类基础之二:相似矩阵
在上一节我们讲到了邻接矩阵 $W$,它是由任意两点之间的权重值 $w_{ij}$ 组成的矩阵。通常我们可以自己输入权重,但是在谱聚类中,我们只有数据点的定义,并没有直接给出这个邻接矩阵,那么怎么得到这个邻接矩阵呢?
基本思想是,距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高,不过这仅仅是定性,我们需要定量的权重值。一般来说,我们可以通过样本点距离度量的相似矩阵 $S$ 来获得邻接矩阵 $W$。
构建邻接矩阵 $W$ 的方法有三类。$\epsilon$-邻近法,K邻近法和全连接法。
对于 $\epsilon$-邻近法,它设置了一个距离阈值 $\epsilon$ ,然后用欧式距离 $s_{ij}$ 度量任意两点 $x_i$ 和 $x_j$ 的距离。即相似矩阵的 $s_{ij} = \Vert x_i-x_j\Vert_2^2$, 然后根据 $s_{ij}$ 和 $\epsilon$ 的大小关系,来定义邻接矩阵 $W$ 如下:
\[w_{ij}= \begin{cases} 0& {s_{ij} > \epsilon}\\ \epsilon& {s_{ij}\leq \epsilon} \end{cases}\]从上式可见,两点间的权重要不就是 $\epsilon$, 要不就是0,没有其他的信息了。距离远近度量很不精确,因此在实际应用中,我们很少使用 $\epsilon$-邻近法。
第二种定义邻接矩阵 $W$ 的方法是K邻近法,利用KNN算法遍历所有的样本点,取每个样本最近的k个点作为近邻,只有和样本距离最近的k个点之间的 $w_{ij} > 0$。但是这种方法会造成重构之后的邻接矩阵W非对称,我们后面的算法需要对称邻接矩阵。为了解决这种问题,一般采取下面两种方法之一:
第一种K邻近法是只要一个点在另一个点的K近邻中,则保留 $s_{ij}$
\[w_{ij}=w_{ji}= \begin{cases} 0& {x_i \notin KNN(x_j) \land x_j \notin KNN(x_i)}\\ \exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2})& {x_i \in KNN(x_j) \lor x_j \in KNN(x_i)} \end{cases}\]第二种K邻近法是必须两个点互为K近邻中,才能保留 $s_{ij}$
\[w_{ij}=w_{ji}= \begin{cases} 0& {x_i \notin KNN(x_j) \lor x_j \notin KNN(x_i)}\\ \exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2})& {x_i \in KNN(x_j) \land x_j \in KNN(x_i)} \end{cases}\]第三种定义邻接矩阵 $W$ 的方法是全连接法,相比前两种方法,第三种方法所有的点之间的权重值都大于0,因此称之为全连接法。可以选择不同的核函数来定义边权重,常用的有多项式核函数,高斯核函数和Sigmoid核函数。最常用的是高斯核函数RBF,此时相似矩阵和邻接矩阵相同:
\[w_{ij}=s_{ij}=\exp(-\frac{||x_i-x_j||_2^2}{2\sigma^2})\]在实际的应用中,使用第三种全连接法来建立邻接矩阵是最普遍的,而在全连接法中使用高斯径向核RBF是最普遍的。
4. 谱聚类基础之三:拉普拉斯矩阵
单独把拉普拉斯矩阵(Graph Laplacians)拿出来介绍是因为后面的算法和这个矩阵的性质息息相关。它的定义很简单,拉普拉斯矩阵 $L= D-W$。$D$ 即为我们第二节讲的度矩阵,它是一个对角矩阵。而 $W$ 即为我们第二节讲的邻接矩阵,它可以由我们第三节的方法构建出。
拉普拉斯矩阵有一些很好的性质如下:
1)拉普拉斯矩阵是对称矩阵,这可以由 $D$ 和 $W$ 都是对称矩阵而得。
2)由于拉普拉斯矩阵是对称矩阵,则它的所有的特征值都是实数。
3)对于任意的向量 $f$,我们有
\[f^TLf = \frac{1}{2}\sum\limits_{i,j=1}^{n}w_{ij}(f_i-f_j)^2\]这个利用拉普拉斯矩阵的定义很容易得到如下:
\[\begin{aligned}f^TLf = &f^TDf - f^TWf = \sum\limits_{i=1}^{n}d_if_i^2 - \sum\limits_{i,j=1}^{n}w_{ij}f_if_j \\ =&\frac{1}{2}(\sum\limits_{i=1}^{n}d_if_i^2 - 2\sum\limits_{i,j=1}^{n}w_{ij}f_if_j + \sum\limits_{j=1}^{n}d_jf_j^2) = \frac{1}{2}\sum\limits_{i,j=1}^{n}w_{ij}(f_i-f_j)^2 \end{aligned}\]4)拉普拉斯矩阵是半正定的,且对应的 $n$ 个实数特征值都大于等于0,即 $0 =\lambda_1 \leq \lambda_2 \leq…\leq \lambda_n$, 且最小的特征值为0,这个由性质3很容易得出。
5. 谱聚类基础之四:无向图切图
对于无向图 $G$ 的切图,我们的目标是将图 $G(V,E)$ 切成相互没有连接的k个子图,每个子图点的集合为:$A_1,A_2,..A_k$,它们满足 $A_i \cap A_j = \emptyset$, 且 $A_1 \cup A_2 \cup … \cup A_k = V$.
对于任意两个子图点的集合 $A, B \subset V$, $A \cap B = \emptyset$ , 我们定义A和B之间的切图权重为:
\[W(A, B) = \sum\limits_{i \in A, j \in B}w_{ij}\]那么对于我们 $k$ 个子图点的集合: $A_1,A_2,..A_k$ ,我们定义切图cut为:
\[cut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}W(A_i, \bar{A}_i)\]其中 $\bar{A}_i$ 为 $A_i$ 的补集,意为除 $A_i$ 子集外其他 $V$ 的子集的并集。
那么如何切图可以让子图内的点权重和高,子图间的点权重和低呢?一个自然的想法就是最小化 $cut(A_1,A_2,…A_k)$, 但是可以发现,这种极小化的切图存在问题,如下图: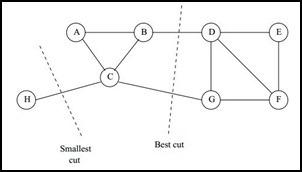
我们选择一个权重最小的边缘的点,比如C和H之间进行cut,这样可以最小化 $cut(A_1,A_2,…A_k)$, 但是却不是最优的切图,如何避免这种切图,并且找到类似图中”Best Cut”这样的最优切图呢?我们下一节就来看看谱聚类使用的切图方法。
6. 谱聚类之切图聚类
为了避免最小切图导致的切图效果不佳,我们需要对每个子图的规模做出限定,一般来说,有两种切图方式,第一种是RatioCut,第二种是Ncut。下面我们分别加以介绍。
6.1 RatioCut切图
RatioCut切图为了避免第五节的最小切图,对每个切图,不光考虑最小化 $cut(A_1,A_2,…A_k)$,它还同时考虑最大化每个子图点的个数,即:
\[RatioCut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}\frac{W(A_i, \bar{A}_i)}{|A_i|}\]那么怎么最小化这个RatioCut函数呢?牛人们发现,RatioCut函数可以通过如下方式表示。
我们引入指示向量 $h_j \in {h_1, h_2,..h_k}, j =1,2,…k$ ,对于任意一个向量 $h_j$, 它是一个 $n$ 维向量($n$ 为样本数),我们定义 $h_{ij}$ 为:
\(h_{ij}= \begin{cases} 0& {v_i \notin A_j}\\ \frac{1}{\sqrt{|A_j|}}& {v_i \in A_j} \end{cases}\)
那么我们对于 $h_i^TLh_i$, 有:
\[\begin{align} h_i^TLh_i & =\frac{1}{2}\sum\limits_{m=1}\sum\limits_{n=1}w_{mn}(h_{im}-h_{in})^2 \\& =\frac{1}{2}(\sum\limits_{m \in A_i, n \notin A_i}w_{mn}(\frac{1}{\sqrt{|A_i|}} - 0)^2 + \sum\limits_{m \notin A_i, n \in A_i}w_{mn}(0 - \frac{1}{\sqrt{|A_i|}} )^2\\& = \frac{1}{2}(\sum\limits_{m \in A_i, n \notin A_i}w_{mn}\frac{1}{|A_i|} + \sum\limits_{m \notin A_i, n \in A_i}w_{mn}\frac{1}{|A_i|}\\& = \frac{1}{2}(cut(A_i, \bar{A}_i) \frac{1}{|A_i|} + cut(\bar{A}_i, A_i) \frac{1}{|A_i|}) \\& = \frac{cut(A_i, \bar{A}_i)}{|A_i|} \end{align}\]上述第1式用了上面第四节的拉普拉斯矩阵的性质3. 第2式用到了指示向量的定义。可以看出,对于某一个子图 $i$,它的RatioCut对应于 $h_i^TLh_i$, 那么我们的 $k$ 个子图呢?对应的RatioCut函数表达式为:
\[RatioCut(A_1,A_2,...A_k) = \sum\limits_{i=1}^{k}h_i^TLh_i = \sum\limits_{i=1}^{k}(H^TLH)_{ii} = tr(H^TLH)\]其中 $tr(H^TLH)$ 为矩阵的迹。也就是说,我们的RatioCut切图,实际上就是最小化我们的 $tr(H^TLH)$。注意到 $H^TH=I$, 则我们的切图优化目标为:
\[\operatorname*{arg\,min}_H\;tr(H^TLH)\text{ s.t. }H^TH=I\]注意到我们 $H$ 矩阵里面的每一个指示向量都是 $n$ 维的,向量中每个变量的取值为0或者 $\frac{1}{\sqrt{\vert A_j\vert}}$,就有 $2^n$ 种取值,有 $k$ 个子图的话就有 $k$ 个指示向量,共有 $k2^n$ 种 $H$,因此找到满足上面优化目标的 $H$ 是一个NP难的问题。那么是不是就没有办法了呢?
注意观察 $tr(H^TLH)$ 中每一个优化子目标 $h_i^TLh_i$, 其中 $h$ 是单位正交基, $L$ 为对称矩阵,此时 $h_i^TLh_i$ 的最大值为 $L$ 的最大特征值,最小值是 $L$ 的最小特征值。如果你对主成分分析PCA很熟悉的话,这里很好理解。在PCA中,我们的目标是找到协方差矩阵(对应此处的拉普拉斯矩阵L)的最大的特征值,而在我们的谱聚类中,我们的目标是找到目标的最小的特征值,得到对应的特征向量,此时对应二分切图效果最佳。也就是说,我们这里要用到维度规约的思想来近似去解决这个NP难的问题。
对于 $h_i^TLh_i$,我们的目标是找到最小的L的特征值,而对于 $tr(H^TLH) = \sum\limits_{i=1}^{k}h_i^TLh_i$ ,则我们的目标就是找到 $k$ 个最小的特征值,一般来说,$k$ 远远小于 $n$,也就是说,此时我们进行了维度规约,将维度从 $n$ 降到了 $k$,从而近似可以解决这个NP难的问题。
通过找到 $L$ 的最小的 $k$ 个特征值,可以得到对应的 $k$ 个特征向量,这 $k$ 个特征向量组成一个 $n\times k$ 维度的矩阵,即为我们的 $H$。一般需要对 $H$ 矩阵按行做标准化,即
\[h_{ij}^{*}= \frac{h_{ij}}{\sqrt{\sum\limits_{t=1}^kh_{it}^{2}}}\]由于我们在使用维度规约的时候损失了少量信息,导致得到的优化后的指示向量 $h$ 对应的 $H$ 现在不能完全指示各样本的归属,因此一般在得到 $n\times k$ 维度的矩阵 $H$ 后还需要对每一行进行一次传统的聚类,比如使用K-Means聚类.
6.2 Ncut切图
Ncut切图和RatioCut切图很类似,但是把Ratiocut的分母 $|Ai|$ 换成 $vol(A_i)$. 由于子图样本的个数多并不一定权重就大,我们切图时基于权重也更合我们的目标,因此一般来说Ncut切图优于RatioCut切图。
\[NCut(A_1,A_2,...A_k) = \frac{1}{2}\sum\limits_{i=1}^{k}\frac{W(A_i, \bar{A}_i)}{vol(A_i)}\]对应的,Ncut切图对指示向量 $h$ 做了改进。注意到RatioCut切图的指示向量使用的是 $\frac{1}{\sqrt{\vert A_j\vert}}$ 标示样本归属,而Ncut切图使用了子图权重 $\frac{1}{\sqrt{vol(A_j)}}$ 来标示指示向量 $h$,定义如下:
\[h_{ij}= \begin{cases} 0& {v_i \notin A_j}\\ \frac{1}{\sqrt{vol(A_j)}}& {v_i \in A_j} \end{cases}\]那么我们对于 $h_i^TLh_i$, 有:
\[\begin{align} h_i^TLh_i & =\frac{1}{2}\sum\limits_{m=1}\sum\limits_{n=1}w_{mn}(h_{im}-h_{in})^2 \\& =\frac{1}{2}(\sum\limits_{m \in A_i, n \notin A_i}w_{mn}(\frac{1}{\sqrt{vol(A_i)}} - 0)^2 + \sum\limits_{m \notin A_i, n \in A_i}w_{mn}(0 - \frac{1}{\sqrt{vol(A_i)}} )^2\\& = \frac{1}{2}(\sum\limits_{m \in A_i, n \notin A_i}w_{mn}\frac{1}{vol(A_i)} + \sum\limits_{m \notin A_i, n \in A_i}w_{mn}\frac{1}{vol(A_i)}\\& = \frac{1}{2}(cut(A_i, \bar{A}_i) \frac{1}{vol(A_i)} + cut(\bar{A}_i, A_i) \frac{1}{vol(A_i)}) \\& = \frac{cut(A_i, \bar{A}_i)}{vol(A_i)} \end{align}\]推导方式和RatioCut完全一致。也就是说,我们的优化目标仍然是
\[NCut(A_1,A_2,...A_k) = \sum\limits_{i=1}^{k}h_i^TLh_i = \sum\limits_{i=1}^{k}(H^TLH)_{ii} = tr(H^TLH)\]但是此时我们的 $H^TH \neq I$, 而是 $H^TDH = I$。推导如下:
\[h_i^TDh_i = \sum\limits_{j=1}^{n}h_{ij}^2d_j =\frac{1}{vol(A_i)}\sum\limits_{j \in A_i}d_j= \frac{1}{vol(A_i)}vol(A_i) =1\]也就是说,此时我们的优化目标最终为:
\[\operatorname*{arg\,min}_H\;tr(H^TLH)\text{ s.t. }H^TDH=I\]此时我们的 $H$ 中的指示向量 $h$ 并不是标准正交基,所以在RatioCut里面的降维思想不能直接用。怎么办呢?其实只需要将指示向量矩阵 $H$ 做一个小小的转化即可。
我们令 $H = D^{-1/2}F$, 则:$H^TLH = F^TD^{-1/2}LD^{-1/2}F$,$H^TDH=F^TF = I$, 也就是说优化目标变成了:
\[\operatorname*{arg\,min}_F\;tr(F^TD^{-1/2}LD^{-1/2}F)\text{ s.t. }F^TF=I\]可以发现这个式子和RatioCut基本一致,只是中间的 $L$ 变成了 $D^{-1/2}LD^{-1/2}$。这样我们就可以继续按照RatioCut的思想,求出 $D^{-1/2}LD^{-1/2}$ 的最小的前 $k$ 个特征值,然后求出对应的特征向量,并标准化,得到最后的特征矩阵 $F$, 最后对 $F$ 进行一次传统的聚类(比如K-Means)即可。
一般来说,$D^{-1/2}LD^{-1/2}$ 相当于对拉普拉斯矩阵 $L$ 做了一次标准化,即 $\frac{L_{ij}}{\sqrt{d_i*d_j}}$
7. 谱聚类算法流程
铺垫了这么久,终于可以总结下谱聚类的基本流程了。一般来说,谱聚类主要的注意点为相似矩阵的生成方式(参见第二节),切图的方式(参见第六节)以及最后的聚类方法(参见第六节)。
最常用的相似矩阵的生成方式是基于高斯核距离的全连接方式,最常用的切图方式是Ncut。而到最后常用的聚类方法为K-Means。下面以Ncut总结谱聚类算法流程。
输入:样本集 $D=(x_1,x_2,…,x_n)$,相似矩阵的生成方式, 降维后的维度 $k_1$, 聚类方法,聚类后的维度 $k_2$
输出: 簇划分 $C(c_1,c_2,…c_{k_2})$.
1)根据输入的相似矩阵的生成方式构建样本的相似矩阵 $S$
2)根据相似矩阵 $S$ 构建邻接矩阵 $W$,构建度矩阵 $D$
3)计算出拉普拉斯矩阵 $L$
4)构建标准化后的拉普拉斯矩阵 $D^{-1/2}LD^{-1/2}$
5)计算 $D^{-1/2}LD^{-1/2}$ 最小的 $k_1$ 个特征值所各自对应的特征向量 $f$
6)将各自对应的特征向量 $f$ 组成的矩阵按行标准化,最终组成 $n\times k_1$ 维的特征矩阵 $F$
7)对 $F$ 中的每一行作为一个 $k_1$ 维的样本,共 $n$ 个样本,用输入的聚类方法进行聚类,聚类维数为 $k_2$。
8)得到簇划分 $C(c_1,c_2,…c_{k_2})$.
8. 谱聚类算法总结
谱聚类算法是一个使用起来简单,但是讲清楚却不是那么容易的算法,它需要你有一定的数学基础。如果你掌握了谱聚类,相信你会对矩阵分析,图论有更深入的理解。同时对降维里的主成分分析也会加深理解。
下面总结下谱聚类算法的优缺点。
谱聚类算法的主要优点有:
1)谱聚类只需要数据之间的相似度矩阵,因此对于处理稀疏数据的聚类很有效。这点传统聚类算法比如K-Means很难做到
2)由于使用了降维,因此在处理高维数据聚类时的复杂度比传统聚类算法好。
谱聚类算法的主要缺点有:
1)如果最终聚类的维度非常高,则由于降维的幅度不够,谱聚类的运行速度和最后的聚类效果均不好。
2)聚类效果依赖于相似矩阵,不同的相似矩阵得到的最终聚类效果可能很不同。